Abstract
Starting from the foundamental principles from classical search methods, such as hill climbing and graph search, we propose a principled and general framework for inference-time scaling of diffusion models through search. Our framework consists of the following components:
- Gradient-driven local search via annealed Langevin MCMC
- Tree-based global exploration via BFS/DFS
We carry out extensive experiments on various tasks, including long horizon maze planning, offline reinforcement learning and image generation, showing that classical search principles could serve as the foundation for inference-time scaling of diffusion models.
Introduction
Diffusion models have demonstrated exceptional performance in generative modeling for continous domains such as images, videos and robotics. However, they still struggles with flexible control at inference time, which is crucial for tasks like planning and reinforcement learning. We approach this challenge from the inference-time scaling perspective, leveraging classical search methods to search the generative space of diffusion models for high quality samples.
As shown in the above demo, we first search the vicinity of the samples via gradient-guided local search. To avoid being stuck in local maximums and OOD samples, we explore the the diverse modes in the multimodal generative space globally, improving the effciency using tree-based search methods such as BFS and DFS. This unfied search framework allows us to efficiently sample from global optimal modes with high quality samples.
Local Search
We fomulate the problem as sampling from the composed distribution of the base distribution \({p}_0(\mathbf{x})\) and the verifier score \(f(\mathbf{x})\):
$$ \tilde{p}_0(\mathbf{x}_0) \propto p_0(\mathbf{x}_0) f(\mathbf{x}_0)^\lambda $$
Through annealed Langevin MCMC, we construct a sequence of distributions \(\tilde{q}_t(\mathbf{x}_t)\) that gradually approaches \(\tilde{p}_0(\mathbf{x}_0)\): $$ \tilde{q}_t(\mathbf{x}_t) \propto q_t(\mathbf{x}_t) \tilde{f}_t(\mathbf{x}_t) $$ where \(q_t(\mathbf{x}_t)\) is the distribution of the diffusion model at time step \(t\), and \(\tilde{f}_t(\mathbf{x}_t)\) is constructed using \(f(\mathbf{x}_{0|t})\). We then sample from the distribution \(\tilde{q}_t(\mathbf{x}_t)\) at each step \(t\) using Langevin dynamics: $$ \mathbf{x}_{t}^{i+1} = \mathbf{x}_t^i + \frac{\epsilon}{2} \nabla_{\mathbf{x}_t} \log \tilde{q}_t(\mathbf{x}_t^i) + \sqrt{\epsilon} \mathbf{z}_t^i\,,~~~\mathbf{z}_t^i\sim\mathcal{N}(\mathbf{0},\mathbf{I}) $$ which can be seen as conducting hill-climbing, following the gradient flow of the KL divergence between \(\tilde{q}_t\) and the distribution of current sample \(\mathbf{x}_t\).
Global Search
To explore diverse modes in the multimodal distribution induced by diffusion models, we view the sampling process as a search tree, and use classical search methods such as breadth-first search (BFS) and depth-first search (DFS) to explore the space efficiently.
This fomulation encompasses other search methods as instances or combinations of BFS and DFS, and through our extensive experiments, we demonstrate the superior efficiency and adaptivity of our search framework compared to existing methods.
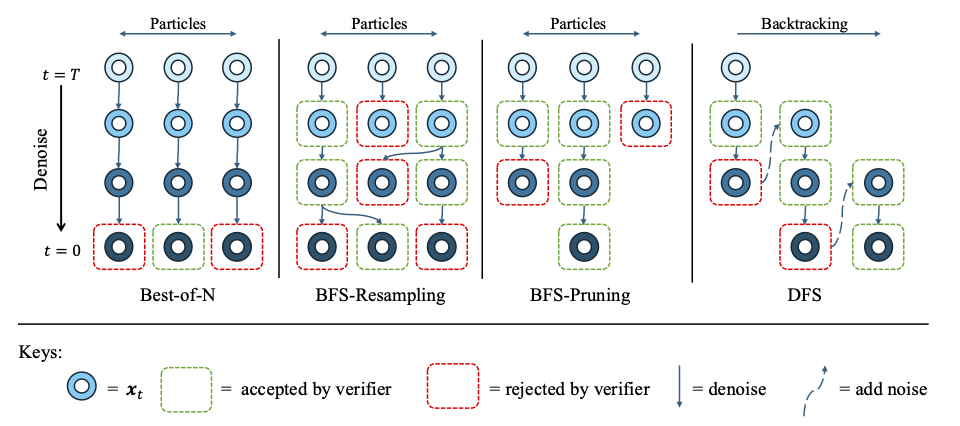
Best-of-N
As a baseline in global search, in Best-of-N, we sample N samples from the diffusion model in paralle, and select the best sample according to the verifier score \(f(\mathbf{x})\). This method is simple and effective, but it does not utilize information from intermediate states, thus being inefficient.
BFS
In BFS, similar to best-first search where we use a heuristic to evaluate intermediate states, we dynamically allocate compute to intermediate particles \(\mathbf{x}_t\) by sampling varying number of children based on their verifier score estimate.
In BFS-Resampling, we sample \(n_t^k\) children for particle \(\mathbf{x}_t^k\) at time step \(t\) propotional to their verifier score: $$ n_t^k = \texttt{Round} \left(N_t\frac{f(\mathbf{x}_{0|t}^k)}{\sum_{j=1}^{N_t} f(\mathbf{x}_{0|t}^j)} \right) $$ where \(N_t\) is the number of particles at time step \(t\).
When using determinstic ODE-solvers as samplers, sampling more than one children from the same particle results in duplication. In BFS-Pruning, we then prune the particles with: $$n_t^k = \min\left(1, \texttt{Round} \left(N_t\frac{f(\mathbf{x}_{0|t}^k)}{\sum_{j=1}^{N_t} f(\mathbf{x}_{0|t}^j)} \right) \right)$$ so we sample at most one children for each parent particle \(\mathbf{x}_t^k\), gradually removing bad samples.
DFS
In DFS, we only denoise one particle, and set a threshold \(\delta_t\) for the verifier score. When the verifier score estimate falls below the threshold: $$ f(\mathbf{x}_{0|t}) < \delta_t $$ we backtrack by adding noise to a higher noise level: $$ t_{\text{next}}=t+\Delta,~~~\mathbf{x}_{t_{\text{next}}} = \mathbf{x}_t + \sqrt{\sigma_{t_{\text{next}}}^2-\sigma_t^2}\mathbf{z}\,,~~~\mathbf{z}\sim\mathcal{N}(\mathbf{0},\mathbf{I})$$ where \(\Delta\) is the backtrack step size.
Experiments
We conduct extensive experiments on various tasks, including long horizon maze planning, offline RL and image generation
Maze Planning
We show that with inference-scaling, diffusion models can succeed in long horizon planning in complex maze environments. We sample from the composed distribution: $$ \tilde{p}_0(\mathbf{\tau}_0) \propto p_0(\mathbf{\tau}_0) \exp{\left(-\lambda L(\mathbf{\tau}_0)\right)}$$ where \( L(\mathbf{\tau}_0) \) measures the collision of the trajectory \(\mathbf{\tau}_0\) with the maze walls, so we minimize the violation of the generated plan.
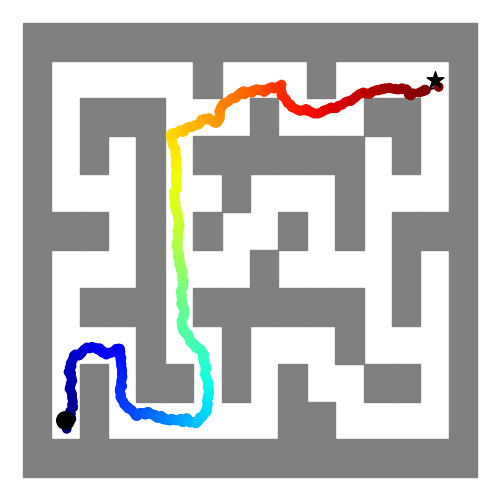
Below, we show with local search, the model is able to generate complex and successful plans.
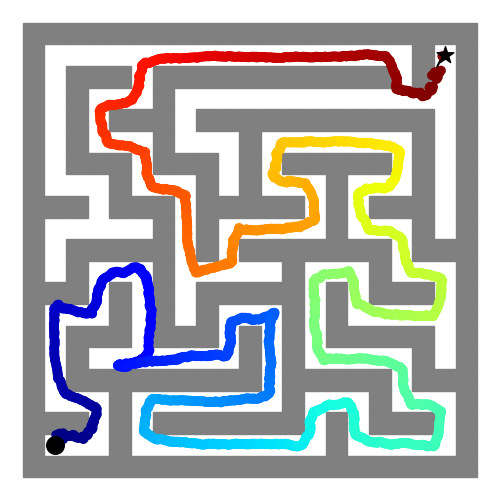
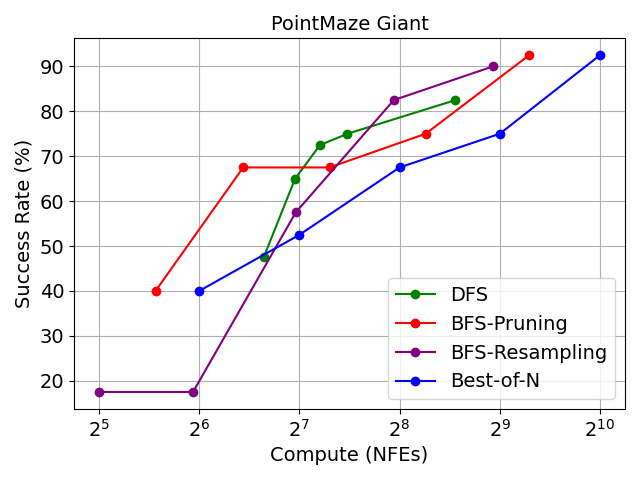
With global search, we can further reach over 80% success rate.
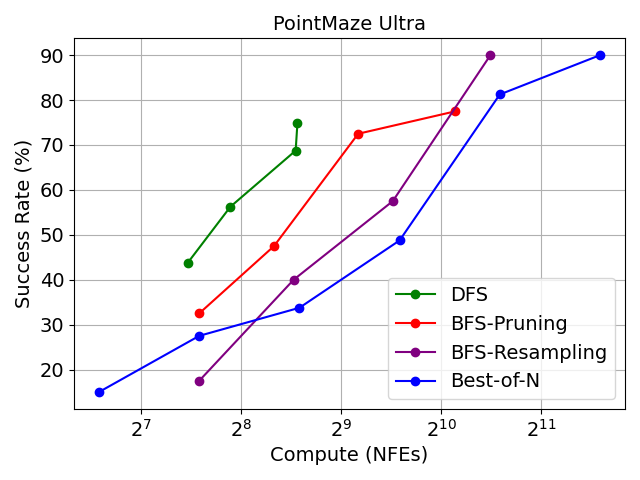
Offline RL
We use a pretrained diffusion model and a pretrained Q-function as verifier for offline RL. We formulate offline RL as sampling from the Q-weighted distribution: $$ \tilde{\pi}(\mathbf{a}_0|\mathbf{s}) \propto \pi(\mathbf{a}_0|\mathbf{s}) \exp\left(\lambda Q(\mathbf{a}_0,\mathbf{s})\right) $$ where \(\pi\) is the pretrained diffusion model, and \(Q\) is the pretrained Q-function.
We evaluate our method on D4RL locomotion tasks. Our training-free method can achieve comparable performance to the state-of-the-art training-required methods.
| Dataset | Environment | CQL | BCQ | IQL | SfBC | DD | Diffuser | D-QL | QGPO | TTS (ours) |
|---|---|---|---|---|---|---|---|---|---|---|
| Medium-Expert | HalfCheetah | 62.4 | 64.7 | 86.7 | 92.6 | 90.6 | 79.8 | 96.1 | 93.5 | 93.9 ± 0.3 |
| Medium-Expert | Hopper | 98.7 | 100.9 | 91.5 | 108.6 | 111.8 | 107.2 | 110.7 | 108.0 | 104.4 ± 3.1 |
| Medium-Expert | Walker2d | 111.0 | 57.5 | 109.6 | 109.8 | 108.8 | 108.4 | 109.7 | 110.7 | 111.4 ± 0.1 |
| Medium | HalfCheetah | 44.4 | 40.7 | 47.4 | 45.9 | 49.1 | 44.2 | 50.6 | 54.1 | 54.8 ± 0.1 |
| Medium | Hopper | 58.0 | 54.5 | 66.3 | 57.1 | 79.3 | 58.5 | 82.4 | 98.0 | 99.5 ± 1.7 |
| Medium | Walker2d | 79.2 | 53.1 | 78.3 | 77.9 | 82.5 | 79.7 | 85.1 | 86.0 | 86.5 ± 0.2 |
| Medium-Replay | HalfCheetah | 46.2 | 38.2 | 44.2 | 37.1 | 39.3 | 42.2 | 47.5 | 47.6 | 47.8 ± 0.4 |
| Medium-Replay | Hopper | 48.6 | 33.1 | 94.7 | 86.2 | 100.0 | 96.8 | 100.7 | 96.9 | 97.4 ± 4.0 |
| Medium-Replay | Walker2d | 26.7 | 15.0 | 73.9 | 65.1 | 75.0 | 61.2 | 94.3 | 84.4 | 79.3 ± 9.7 |
| Average (Locomotion) | 63.9 | 51.9 | 76.9 | 75.6 | 81.8 | 75.3 | 86.3 | 86.6 | 86.1 | |
Image Generation
We evaluate our method on compositional text-to-image generation on CompBench, and class conditional ImageNet generation using an unconditional diffusion model with a pretrained classifier.
In compositional test-to-image, we show that inference-time search against a pretrained visual verifier such as UniDet and BLIP can generate images with complex compositional prompts.
Below show the results of prompt "eight bottles" with and without inference scaling, which requires the model to generate the correct number of objects. We use a UniDet Model to count the number of objects in the generated image. After inference scaling the number of bottles in the generated image follows the prompt, while without inference scaling the number of bottles is not consistent with the prompt.


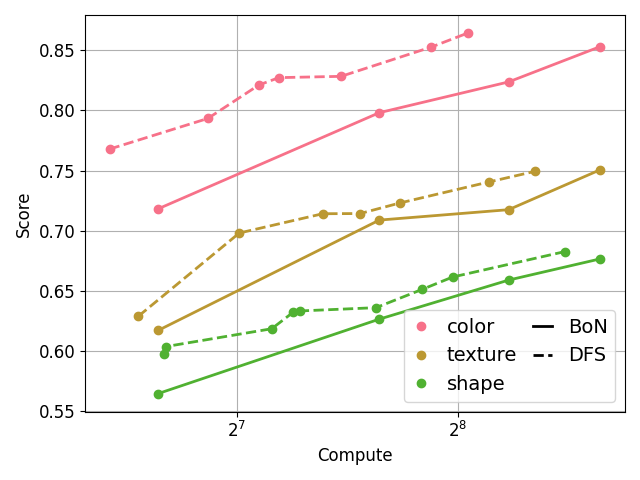
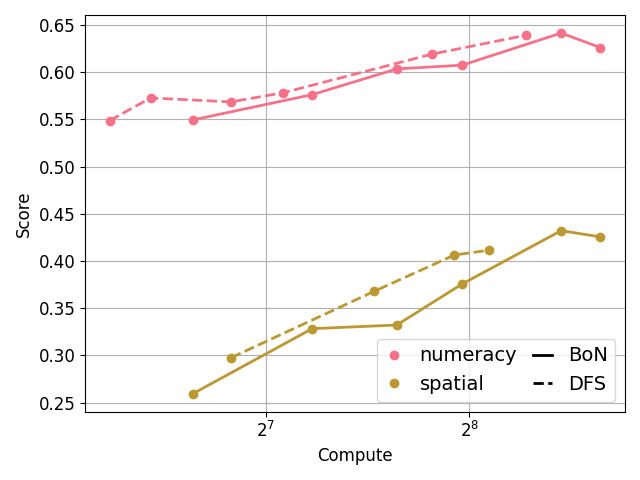
Below is the scaling curve of DFS on the 5 datasets in the attribute binding and object relationship tasks.
In class-conditional image generation, we generate samples aligned with a target class label using an unconditional diffusion model guided by a pretrained ViT classifier as a verifier. $$\tilde{p}_0(\mathbf{x}_0) \propto p_0(\mathbf{x}_0) p\left(c|\mathbf{x}_0\right)$$ Below, we show the uncurated samples for class 222 (“kuvasz”) on ImageNet, demonstrating diverse samples that accurately reflect the class label.

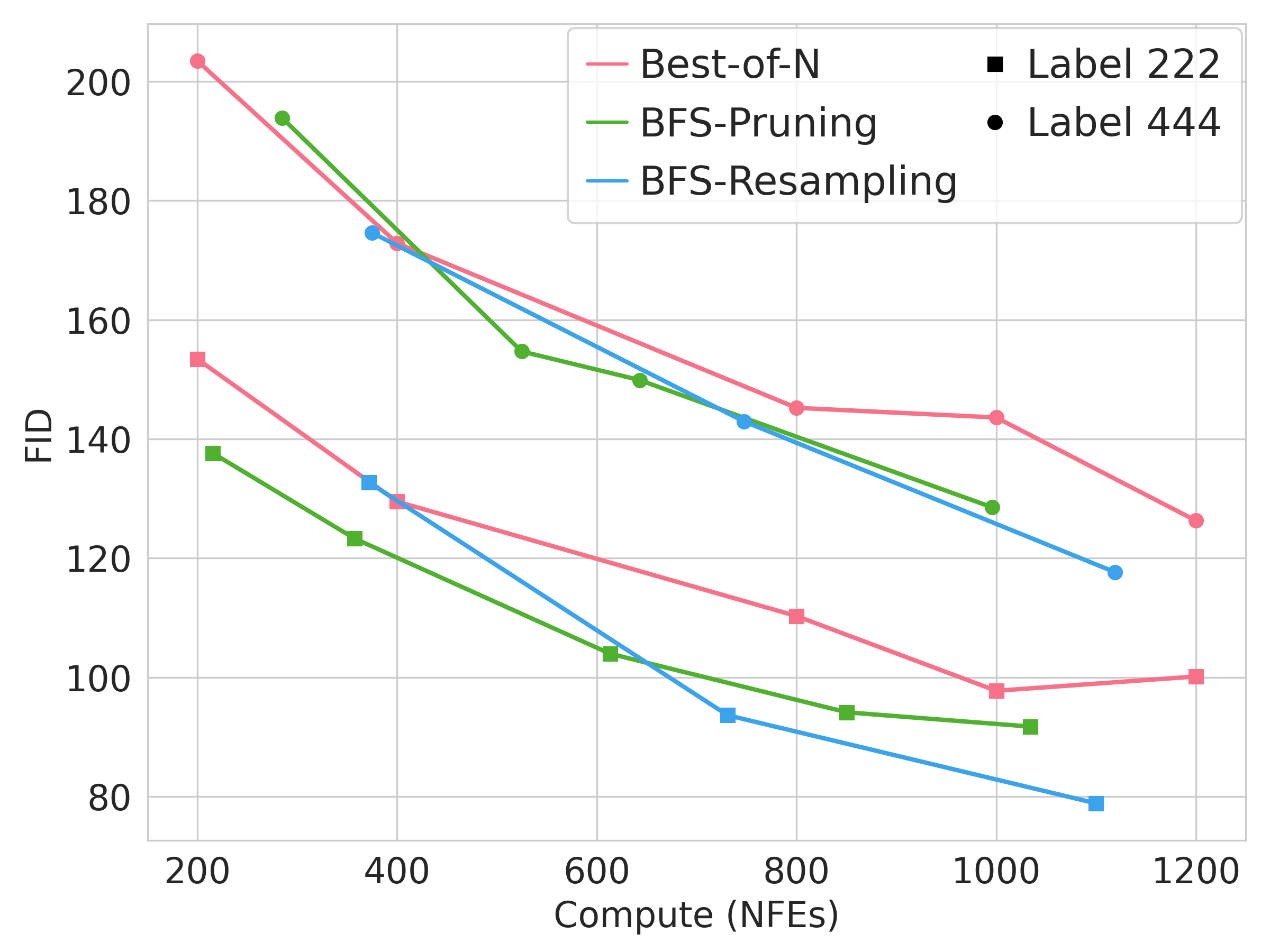
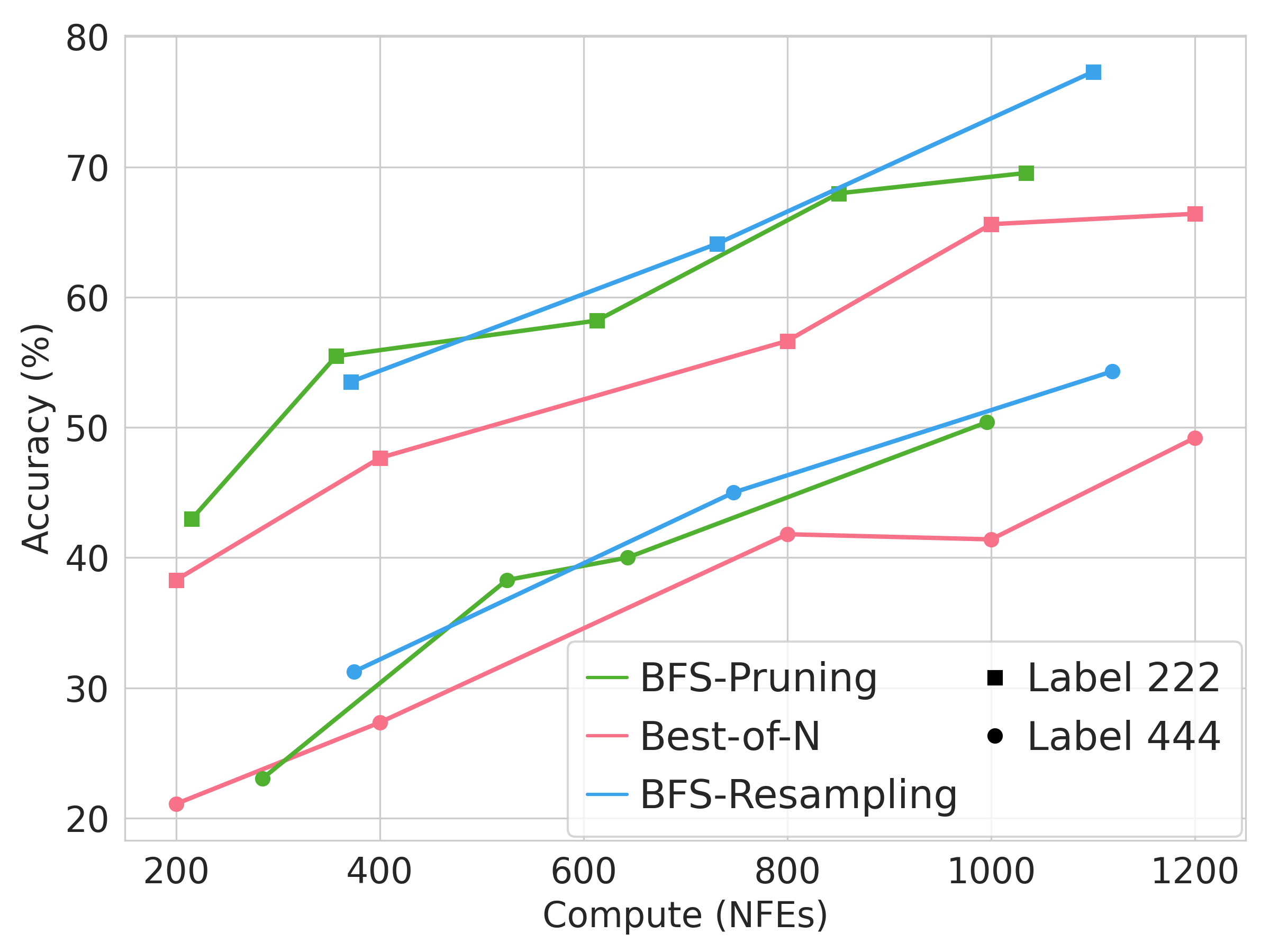
Below is the scaling curve of BFS on ImageNet, showing FID and class accuracy over 256 samples.
Conclusion
We propose a principled and general framework for inference-time scaling of diffusion models through search, which can be applied to various tasks such as planning, reinforcement learning and image generation. Still, inference-time base approaches require more hyper-parameter tuning than naive sampling, which we leave as a future work
Citation
@misc{zhang2025inferencetimescalingdiffusionmodels,
title={Inference-time Scaling of Diffusion Models through Classical Search},
author={Xiangcheng Zhang and Haowei Lin and Haotian Ye and James Zou and Jianzhu Ma and Yitao Liang and Yilun Du},
year={2025},
eprint={2505.23614},
archivePrefix={arXiv},
primaryClass={cs.LG},
url={https://arxiv.org/abs/2505.23614},
}